
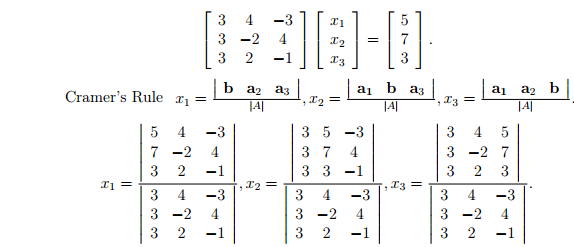
- #Matrix multiplication symbolic calculator how to
- #Matrix multiplication symbolic calculator generator
(See also an excellent research made by Søren Fuglede Jørgensen.)
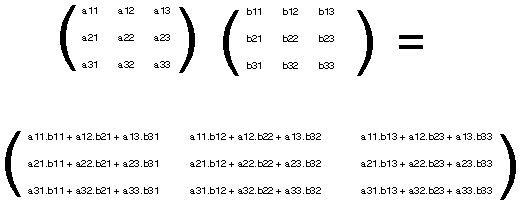
NET community ( #5974, #12746, #23298) but the code remains as is for the sake of backward compatibility. This issue has been discussed many times by the open source. In fact, I don't know any theoretical estimate of the period length for these lags. NET implementation of this algorithm: lag values specified in the code don't guarantee the longest period possible. Besides that, a critical bug has been found in the. First of all, statistical testing exposed some problems immanent to the whole family of lagged Fibonacci generators. Why do we need one more RNG algorithm? Unfortunately, System.Random is not perfect.
#Matrix multiplication symbolic calculator generator
The exception is made for code generator in Haskell: assuming this language is not widely used, I stepped through each line of the code explaining it in more details. For the same reason, I will focus on math background and general ideas rather than software implementation. Part 1 is dedicated to matrix-based approach, while part 2 will consider the polynomial-based algorithm and performance testing. Putting all the material in a single article would made it a bit too long to read at once, so I've decided to split it into two parts. Finally, we will compare these two approaches. After that, we will consider another method of jumping based on polynomial arithmetics which has been mentioned in the previous article but not tried yet. Giving a test drive to Haskell was one of my goals for this research and it appeared to be worth the efforts. This calculation is performed by a program written in a powerful but not very popular language, Haskell. Unlike lagged Fibonacci generators, these matrices have more complex structure so we would prefer to calculate them automatically. We will start from building transition matrices for this RNG. This time, we are going to develop similar functionality for another family of linear RNGs, known as xorshift.
#Matrix multiplication symbolic calculator how to
Using the theory of linear RNGs, we learned how to navigate the sequence of random numbers jumping \(N\) steps forward or backward with logarithmic complexity. This article is a sequel to System.Random and Infinite Monkey Theorem, where we explored the internal structure of the standard random number generator (RNG) from the.


 0 kommentar(er)
0 kommentar(er)
